研究モチベーション
変圧器は非常に身近で、電力を安全/安定に利用するためにはなくてはならない電気機械であるが、電気回路理論の一丁目一番地に位置するY行列との親和性が以下にもまとめるように高くないために、変圧器モデルの回路計算における考察にはまだ多くの余地があると思う。事務所代表がインターネットを検索したところ、二巻線変圧器をY行列に組み込む以下の定式化を発見したが、汎用的な回路計算への統合への拡張は困難であると見受けた。
https://vismor.com/documents/power_systems/transformers/transformer_model.php
もちろん電力系統解析(潮流計算や過渡安定性解析等)においては、単位法の導入により変圧器モデリングについては、適切な形で整理されている。しかし、電圧レベルの低い高圧/低圧回路においては、単位法を導入したところでフィールドの課題を解決する計算機のよる計算の合理化にはつながらない。例えば、多分一番利用形態の多い単相三線式変圧器周りの回路計算を計算機で行おうとしても、Y行列を構築できないので、個別の回路毎に手間をかけする必要がある。事務所代表としては、分散型電源など、様々な回路形態が想定される現在、線形連立方程式を解くだけで高圧/低圧回路の回路計算を実現し、多くのフィールドエンジニアが計算機による電気現象分析の合理化の恩恵に与れないかと昔から考えていた。
今般、電車に乗っているときに、Y行列を変圧器モデルを組み込むべく拡張(GTNA: General Transformer Nodal Analysis)できることを想起したことから、ここに取りまとめ諸賢に真贋の確認をいただくべくここに取りまとめた。
回路計算における一般的な変圧器の扱い
変圧器は巻線間で同じ磁束を共有することで、コイル巻線数に比例した誘導起電力を発生させることで交流電圧の大きさを比較的容易に変成することができる。また、磁束はコイル端子間の電圧により決定されるものであるから、巻線電流による起磁力は当然キャンセルされなければならないから、巻線毎の巻線数と当該巻線電流の積を合計すれば零になる。
一般のテキストには、この原理に基づき回路計算中の変圧器の取り扱いに関しては、巻線比に基づくインピーダンス換算を行う方法が説明されている。しかし、三巻線変圧器や単相三線式変圧器のように2を超えるコイルで磁束を共有するような場合には、インピーダンス換算は不可能であることから、線形方程式を解くだけの回路計算に帰着することできず、計算機による労力の合理化が困難になる。
変圧器を取り扱うためのY行列の拡張
ここでは三巻線変圧器を例にとり、定式化の概要を説明する。
図のように3つの独立した電気回路が一つの三巻線変圧器に接続されているとする。
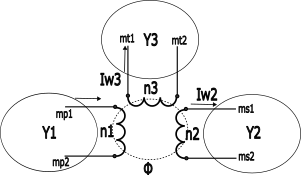
ここで、Y1,Y2,Y3はそれぞれ一次、二次、三次巻線接続回路のY行列である。ここでは二次コイル電流Iw2と三次コイル電流Iw3と磁束Φを未知数に加えることで変圧器モデルをY行列に組み込むことが可能であることを確認した。拡張したY行列は以下のような形式になる。
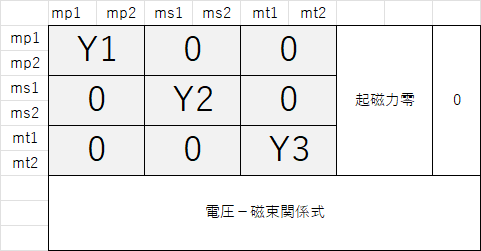
詳細については、問い合わせ先からご連絡をいただければ、別途提供するが、多くの諸賢各位はすぐに追試できるであろう。
例題
最近は便利になりPython in EXCELなる環境が少ないライセンス費用で利用できる。ここでは、以の下単相三線式のモデルの回路計算がここに示した定式化とこのPython in EXCELで計算できたことをご紹介する。まだ、未システム化故、データ入力と結果整理には手間がかかるが適切なシステム化を施せば、多くの便利な機能を実現できるものと確信している
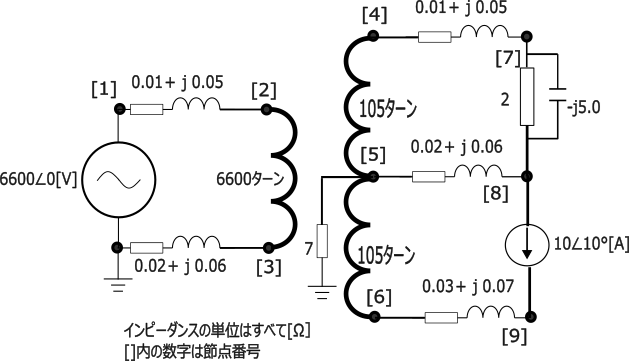
計算結果は以下のテーブルのようになる。
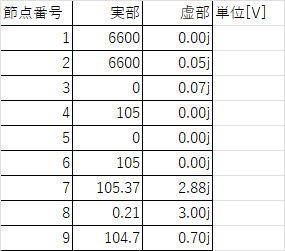
節点電圧の実質的な計算は、(もちろんであるが)以下のコードのみである。
実質的なコマンド(Numpyを活用)
V3=np.linalg.solve(Y3,I3)
なお、単相の三巻線変圧器の検証はもちろん、オープンデルタ結線のEVTやその他の各種結線の三相変圧器についても問題ないことを確認した。地絡時に発生するオープンデルタ端電圧は、完全地絡なら難しくないが、どの程度の地絡抵抗の場合にどの程度の電圧が発生するかを自己研究する際に役に立っている。
可能性
本定式化は、変圧比の大きいような場合は条件数の悪化の悪影響などが想定されるが、故障解析などにおいては、解析者の有効な道具になると思われる。
また、変圧器磁束を直接解いているので、少し工夫すると鉄心飽和も総合的に取り扱うことが可能になると思われる。
もし、社会に広く活用できそうだとお考えの諸賢各位がおられたらご連絡をいただければ幸いである。
